场论里的拓扑

在物理学研究中，高深的数学概念或许并不能告诉你更多新规律，比如实验物理学家，或许不需要太高深的数学知识就能发现很多深刻的物理现象。但是，数学概念的好处在于他的定义足够广泛，使得足够多的对象能纳入里面，这也使得，物理，化学，生物，经济等都能纳入统一的数学框架内，这种统一性正是人们所苦苦追寻的。

这章内容主要来源于Nicholas Manton和Paul Sutcliffe写的《Topological Solitons》的Topology in field theory，我觉得这本书写的很好，所以我对这部分内容进行了一些归纳。

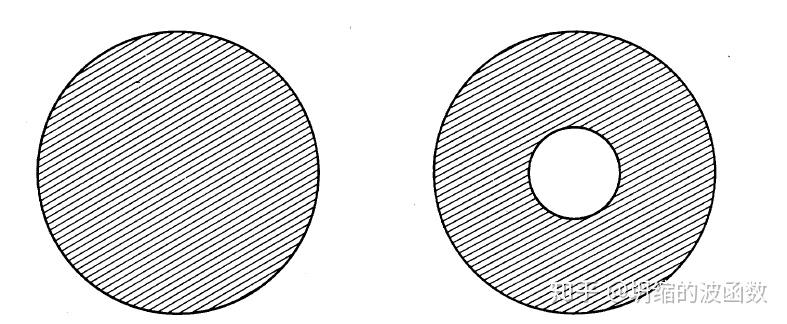
前面内容已经介绍过，为了对圆盘和环这样的对象进行拓扑分类，我们需要刻画洞性质的拓扑不变量，容易看出，圆盘内任意的一条闭曲线都可以连续地收缩到一点，但是环面上一些闭曲线（包围洞的闭曲线）却不能连续收缩到一点。因此，庞加莱提出利用这些闭曲线构成的群来区分这类拓扑空间。此外，我们可以根据闭曲线性质定义等价关系，从而把群划分成不同的等价类。例如：

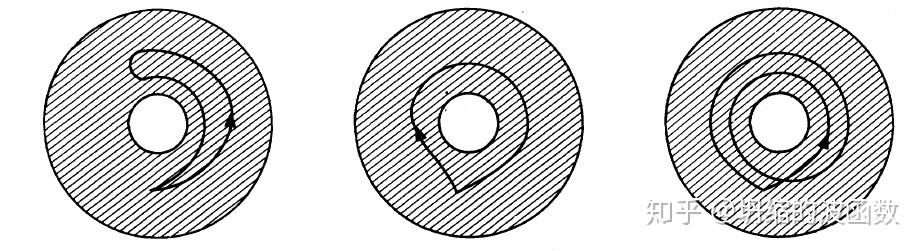
我们可以把最左边能连续收缩到一个点的一类曲线划分为一个等价类，中间环绕洞一圈的一类曲线划分为一个等价类，，最右边环绕洞两圈的一类闭曲线划分为一个等价类......

数学上，这个群上的等价关系是同伦，他描述了这些闭曲线之间的连续形变，如果我们把闭曲线看作是单位区间 到集合（环面，圆盘）上的映射，那么同伦关系便可以扩展为映射之间的等价关系。

如果两个映射 （从集合 映射到 ）是同伦的，我们记为 ，我们把所有与映射 同伦的映射放入一个集合中，这个集合便是同伦等价类，记为 。

要构建一个群，我们便要构建一种代数法则（群乘），由于同伦满足函数的合成关系：

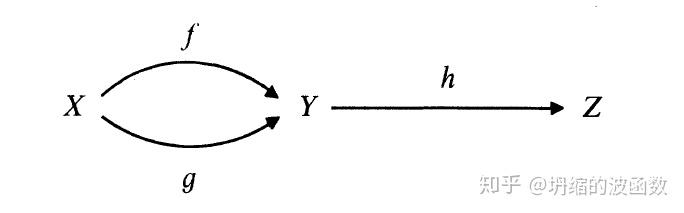
即： ，因此我们可以把群乘定义为同伦等价类的乘法：

这样的乘法关系是满足结合律，并存在单位元和逆元，这样便构成了一个群。

更多时候，我们考虑的是集合 内的闭合回路：

如果 是一个连续映射，使得 ，我们称 是 上基于 点的闭合回路。

由于回路是闭合的，一般的，我们也可以直接把回路看作是圆 到集合 的连续映射。

集合 中的基于点 的闭合回路同伦等价类，在群乘 下形成一个群。

这个群便称为集合 的基本群（第一同伦群），记为 。

很显然圆盘上所有的回路都是同伦等价的，因此他的基本群是平凡的（只有单位元的群），更一般的，所有单连通的集合 ，他的基本群 ，其中 是单位元。这时候，我们便能把单连通拓扑空间和其他的拓扑空间区分开来。例如， ， 。这里 表示整数集， 表示甜甜圈面。

更多时候，我们需要更高的同伦群，例如我们考虑映射 ，研究这样的映射同伦关系构成的群就是第 同伦群，记为 。

这里有个重要的结果： 。

在实际研究场的时候，我们都是研究 空间的映射，由于 与 是不同胚的， 才是与 同胚的。 是 的北极点。这时候我们需要把 的无穷远点粘起来变成一个点，这时候， 与 是同胚的。形象的理解就是实数轴两端粘起来变成了一个圆。以粘起来的 为基础的映射 就是与球面上的映射 是同伦的。

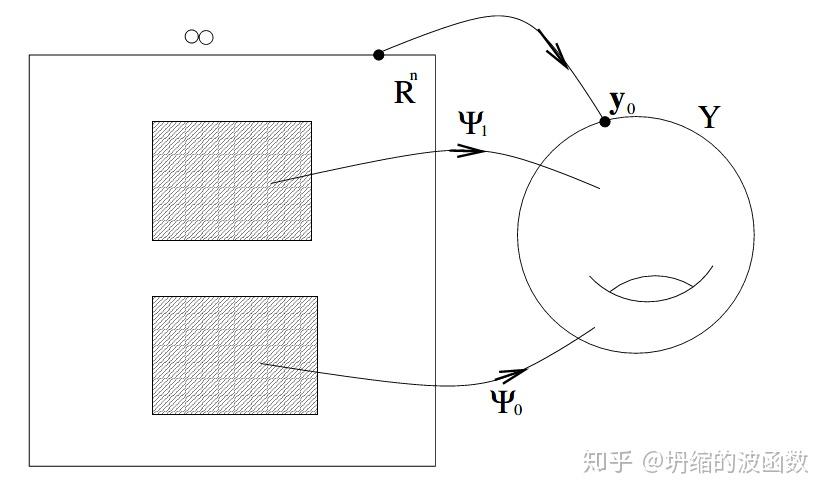
把 粘起来以后便对映射有边界约束，即 ，也就是说无穷远点的映射与球面北极点的映射是相同的。

有了这样的边界条件以后，同伦理论便可以直接应用于标量场理论，场 ，其中 是实数集表示时间流形， 表示空间流形，拉格朗日量可以由这个标量场 给出。如果场满足场方程，那么他在时空上是连续的，因此场的同伦等价类是不随时间改变的，这时候同伦等价类便是一个拓扑守恒量。这也就是之前我们看到的拓扑电荷的概念。

(有些翻译可能不准确，我把英文名也给出)

拓扑度是一个有更多限制的概念，但也是一个比同伦理论更精确的工具，他使我们能够计算确定条件下映射的同伦等价类。

假设有映射 ， 均是连通的维数相等的闭流形， ,并且映射是处处可微以及处处有连续的导数。此外我们还假设定义于 上的归一的体积形式（normalized volume form）

如果 ， 由函数 给出，定义量 ，那么映射 的拓扑度由下式给出：

拓扑度是整数，并且拓扑度是映射 的同伦不变量，因为在连续形变下整数是不变的。此外拓扑度也是独立于 的选择。

其中最重要的例子是映射 ，如果 在同伦群 的第 个同伦类里，那么 。

特别的对于： ，我们选取体积形式 ， 是 上的角坐标，映射由连续函数 给出，那么拓扑度可以表示为

在更高维的流形中，拓扑度也称为绕数。

这里只给出阿贝尔规范场，非阿贝尔规范场书上也有。

研究规范场的拓扑性质时，一般把规范势和场张量看作是微分形式。首先，考虑定义在具有局域坐标 的流形 上的规范场，这里我们忽略了时间依赖。由于规范势是秩为1的协变张量，这意味着，规范势分量 在坐标变换 ，依据下式进行变换：

规范势分量可以与微分1形式联系起来（differential 1-form）

1形式是坐标不变的： 。场张量分量可以与2形式场强联系起来：

这里 表示 的外导数，根据外导数算符的Leibniz规则： ，这里 是 形式（r-form），外导数算符作用两次，有 。

因此 是闭的。在规范变换下：

是规范不变的。因为：

。

阿贝尔规范场的第一陈形式（the first Chern form）可以定义为2形式：

考虑平面 上的规范场，第一陈数可以写成：

如果 是光滑的，并且在 时比 更快趋于0，则 是有限的。并且：

这里 是平面上的磁场。利用微分形式的斯托克斯定理，陈数可以表示为无穷远处圆上的线积分：

这里 是平面极坐标。

由于在无穷远处场强 ，这时候规范势在无穷远处可以表示为纯规范 ，此时

这时，在平面上， 可以取任意值。因为 没必要是单值的，也没必要在无穷远处是 的整数倍。这在物理上不是非常感兴趣的，但是对于标量场的规范势有一些约束的话，那么陈数就必须是整数。

假设 是紧的没边界的二维曲面，一个标量场和 规范场定义于 上。如果我们要求 是全局定义良好的函数和1形式，那么场强 将是恰当2形式，我们将有

表示 的边界，因为 没有边界，所以积分必须等于0。这在物理上也不是非常感兴趣的。更有趣的情形是他们被看作曲面 上 丛的截面（section）和联络（connection）。这里不对这些数学名词进行解释，在物理上， 和 不是可观测的，只有他们的规范等价类才是可观测的。我们想象 有一系列坐标补片 覆盖：

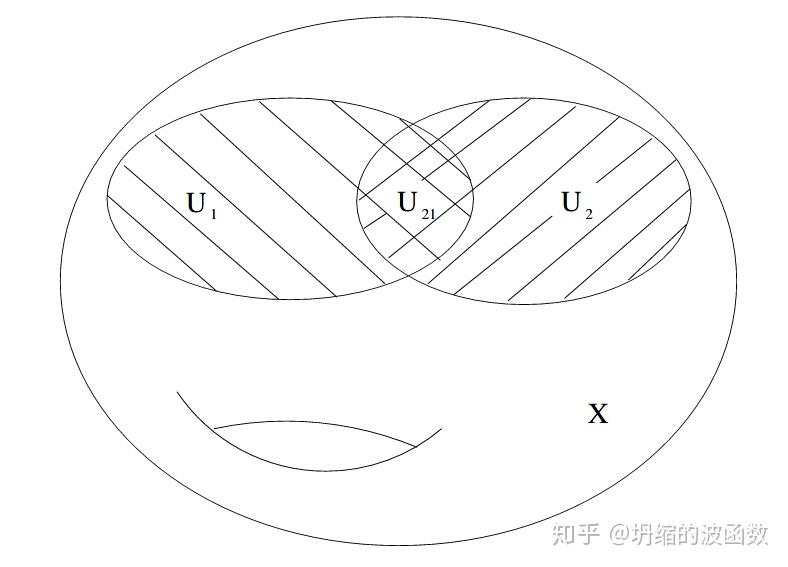
在 上， 写为 ，在 上写为 ，而在 上，我们要求：

其中 只在 上有定义。对于 上定义良好的丛，对于区域 ，存在约束：

由于 ，所以 是全局定义良好的，而且场强也是全局定义良好的。

由于局域上 ，所以 是闭的2形式，满足 。但此时 不是全局定义良好的，所以 不一定是恰当2形式。这时候场强 在 上的积分非零。但是由于存在不同坐标补片交集区的约束关系，这就导致了积分也不可能是任意值。可以证明：

第一陈数是整数。

更一般的，对于紧的没有边界的黎曼闭曲面 ，陈数：

是任意整数。